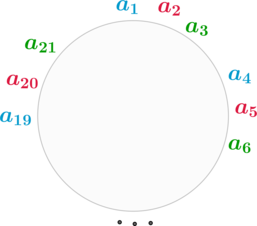Вдоль окружности расставлено 100 натуральных чисел докажите что
Задачи Санкт-Петербургской олимпиады школьников по математике.
В целях развития у учащихся интереса к математике проводятся математические олимпиады различных уровней. Умение решать задачи, особенно олимпиадные, всегда являлось одним из показателей математической одаренности ученика. Недаром многие вузы для победителей и призеров различного уровня олимпиад устанавливают льготы. Многие часто представляют математические олимпиады как соревнование на «самого умного математика школы города, области, … ». Будь это так, олимпиады не стоили бы десятой доли тех усилий, которые вкладываются в них.












Попробуйте повторить позже. Двое игроков ставят крестики и нолики на бесконечной клетчатой бумаге, причём на каждый крестик первого игрока второй отвечает ноликами. Докажите, что первый может добиться, чтобы некоторые четыре крестика образовали квадрат со сторонами, параллельными линиям клеток. Подсказка 1. Каким свойствами должен обладать предпоследний ход первого игрока, если последний является победным? Подсказка 2.
- Затем часть чисел заменили нулями.
- Информация для участников. Устный тур.







/Разговоры о важном/wXo5kQYUPLBC0iaYyQYg.png)